The PLONK IOP for general circuits

• PLONK: a poly-IOP for a general circuit $C(x,w)$
  • Step 1: compile circuit to a computation trace (gate fan-in=2)
    • Encoding the trace as a polynomial
  • Step 2: proving validity of $T$
    • Proving (1): T encodes the correct inputs
    • Proving (2): every gate is evaluated correctly
    • Proving (3): the wiring is correct
• The complete Plonk Poly-IOP (and SNARK)

PLONK: a poly-IOP for a general circuit $C(x,w)$

Step 1: compile circuit to a computation trace (gate fan-in=2)

The computation trace (arithmetization):

Encoding the trace as a polynomial

Notion:
$|C|:=\text{total \# of gates in }C$, $|I|:=|I_x|+|I_w|=\text{\# inputs to }C$
let $d:=3|C|+|I|$ (in example, $d=12$) and $\Omega :=\{1,\omega ,{\omega }^2,\dots ,{\omega }^{d-1}\}$

The plan:
prover interpolates a polynomial $T\in {\mathbb{F}}_p^{(\le d)}[X]$ that encodes the entire trace.

Prover interpolates $T\in {\mathbb{F}}_p^{(\le d)}[X]$ such that
(1) $T$ encodes all inputs: $T({\omega }^{-j})=\text{input \#j}$ for $j=1,\dots ,|I|$
(2) $T$ encodes all wires: $\forall l=0,\dots ,|C|-1$:

• $T({\omega }^{3l}):$ left input to gate #$l$
• $T({\omega }^{3l+1}):$ right input to gate #$l$
• $T({\omega }^{3l+2}):$ output of gate #$l$

In the example, Prover interpolates $T(X)$ such that:

degree($T$) = 11
Prover can use IFFT to compute coefficients of $T$ in time $O(d\log d)$

Step 2: proving validity of $T$

Prover needs to prove that $T$ is a correct computation trace:
(1) $T$ encodes the correct inputs,
(2) every gate is evaluated correctly,
(3) the wiring is implemented correctly,
(4) the output of last gate is 0

Proving (4) is easy: prove $T({\omega }^{3|C|-1})=0$

Proving (1): T encodes the correct inputs

Both prover and verifier interpolate a polynomial $v(X)\in {\mathbb{F}}_p^{(\le |I_x|)}[X]$ that encodes the $x$-inputs to the circuit:
$$\text{for }j=1,\dots ,|I_x|:v({\omega }^{-j})=\text{input\#j}$$

In the example: $v({\omega }^{-1})=5,v({\omega }^{-2})=6.$ ($v$ is linear)
constructing $v(X)$ takes time proportional to the size of input $x$ $\Rightarrow$ verifier has time do this.

Let ${\Omega }_{inp}:=\{{\omega }^{-1},{\omega }^{-2},\dots ,{\omega }^{-|I_x|}\}\subseteq \Omega$ (points encoding the input)
Prover proves (1) by using a ZeroTest on ${\Omega }_{inp}$ to prove that
$$T(y)-v(y)=0\forall y\in {\Omega }_{inp}$$

Lemma: $f$ is zero on $\Omega$ if and only if $f(X)$ is divisible by $Z_{\Omega }(X)$

Proving (2): every gate is evaluated correctly

Idea: encode gate types using a $selector$ polynomial $S(X)$
define $S(X)\in {\mathbb{F}}_p^{(\le d)}[X]$ such that $\forall l=0,\dots ,|C|-1$:

• $S({\omega }^{3l})=1$ if gate #l is an addition gate
• $S({\omega }^{3l})=0$ if gate #l is a multiplication gate

Then $\forall y\in {\Omega }_{gates}:=\{1,{\omega }^3,{\omega }^6,{\omega }^9,\dots ,{\omega }^{3(|C|-1)}\}$:
$$S(y)\cdot [T(y)+T(\omega y)]+(1-S(y))\cdot T(y)\cdot T(\omega y)=T({\omega }^{w}y)$$
Prover uses ZeroTest to prove that for all $\forall y\in {\Omega }_{gates}$: $$S(y)\cdot [T(y)+T(\omega y)]+(1-S(y))\cdot T(y)\cdot T(\omega y)-T({\omega }^{w}y)=$$

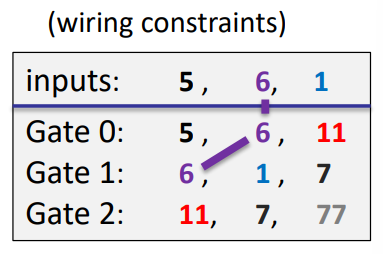
Proving (3): the wiring is correct

encode the wires of $C$:
$$\{\begin{array}{l}T({\omega }^{-2})=T({\omega }^1)=T({\omega }^3)\\ T({\omega }^{-1})=T({\omega }^0)\\ T({\omega }^2)=T({\omega }^6)\\ T({\omega }^{-3})=T({\omega }^4)\\ T({\omega }^5)=T({\omega }^7)\end{array}$$
Define a polynomial $W:\Omega \to \Omega$ that implements a rotation: $$W({\omega }^{-2},{\omega }^1,{\omega }^3)=({\omega }^1,{\omega }^3,{\omega }^{-2}),W({\omega }^{-1},{\omega }^0)=({\omega }^0,{\omega }^{-1}),\dots$$
Lemma: $\forall y\in \Omega :T(y)=T(W(y))\Rightarrow$ wire constraints are satisfied

The complete Plonk Poly-IOP (and SNARK)

Prover proves:
gates: (1) $S(y)\cdot [T(y)+T(\omega y)]+(1-S(y))\cdot T(y)\cdot T(\omega y)-T({\omega }^{2}y)=0\forall y\in {\Omega }_{gates}$
inputs: (2) $T(y)-v(y)=0\forall y\in {\Omega }_{inp}$
wires: (3) $T(y)-T(W(y))=0\text{ (using prescribed perm.check) }\forall y\in \Omega$
output: (4) $T({\omega }^{3|C|-1})=0\text{ output of last gate = 0 }$